|
|
P7926 「EVOI-RD2」大胃王
写在前面:本篇文章不会讲解斜率优化的基本原理。
题目大意:将一个数列分成若干段,每段的价值是这段元素之和减去 L 的平方(先减 L 再平方),定义一个数列的价值为每段的价值之和,对于每个 i ,输出由第 1\sim i 个元素组成的数列 (1 \leq i\leq n) 的最小和非严格次小价值。
记 f_i、g_i 分别为前 i 个元素的最小、次小价值。
显然的 dp 方程, 若i 为当前元素, j 为 f 转移至 f 的最优决策点,有:
f_i=f_j+(s_i-s_j-L)^2\;\;\;\;\;\;\;\;\;\;(0\leq j <i)
j 为 g 转移至 g 的最优抉择点, k 为由 f 转移至 f 的次优决策点。
g_i=min\{g_j+(s_i-s_j-L)^2, f_k+(s_i-s_k-L)^2\}\;\;\;\;\;\;\;\;\;\;(0\leq j,k <i)
接下来是比较重要的部分,而且我不会(懒得)证明正确性,偷一个洛谷的图(侵删)。
首先对于 f 对 f 以及 g 对 g 自身的最优转移我们维护两个下凸壳。
以 f 举例:
移项得 f_i-s_i^2-L^2+2 \times s_i \times L=f_j+s_j^2+2\times s_j\times L-2\times s_i\times s_j
整理得 \begin{equation} \left\{ \begin{aligned} &y_j=f_j+s_j^2+2\times s_j\times L\\ &x_j=s_j\\ &k_i=2\times s_i\\ &b_i= f_i-s_i^2-L^2+2\times s_i\times L \end{aligned} \right. \end{equation}
发现 k、x 均随下标单增,且要维护最小值,单调队列维护下凸壳即可。
考虑 f 到 f 的次优决策点,结论是,次优决策点是 f 自身转移凸壳中的最优决策点的左右两个相邻点,以及从 f 自身转移的凸壳中弹出的所有点构成的另外一个凸壳中的最优决策点,这三个点中的最优点。
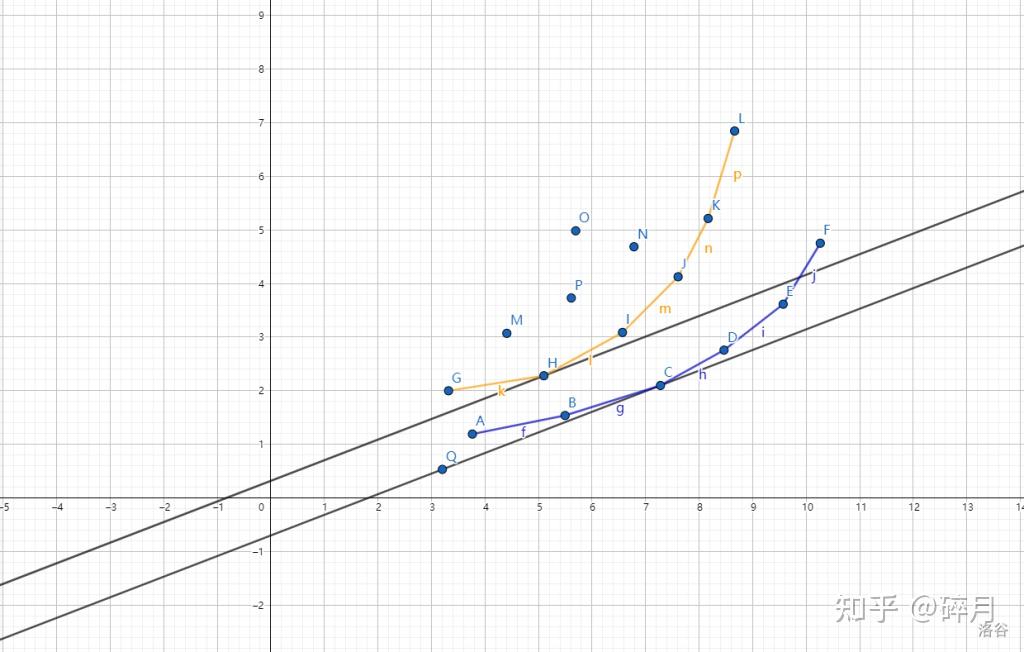
如图, C 是 f 到 f 的最优决策点,那么次优决策点就是 B、D、H 三者中的最优点。
对于图中黄色凸壳的维护,我们需要将蓝色凸壳中弹出的点的序列逆序插入黄色凸壳,在插入前要先将横坐标超出当前要插入的点中的最小横坐标的点删除,他们显然不应该再出现在黄色凸壳上,且不这样特殊处理会出错。
另外我写斜率优化由于精度原因不喜欢用 double 存斜率,所以会导致代码有些冗余,代码看似不长,其实细节很多,下标究竟是队列的下标还是元素的下标要分清。
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
using i64 = long long;
const int N = 200010;
const i64 INF = 1e18;
int n, L;
int a[N];
i64 s[N];
i64 f[N], g[N];
struct Queue {
int q[N];
int tt, hh;
Queue() {
tt = -1, hh = 0;
}
int& operator[](int i) {
return q;
}
} q0, q1, q2;
i64 sq(int x) {
return 1ll * x * x;
}
i64 y(int i) {
return f + sq(s) + 2 * s * L;
}
i64 y2(int i) {
return g + sq(s) + 2 * s * L;
}
i64 x(int i) {
return s;
}
int main() {
cin.tie(0)->sync_with_stdio(false);
cin >> n >> L;
for (int i = 1; i <= n; i++) cin >> a;
for (int i = 1; i <= n; i++) s = s[i - 1] + a;
q0[++q0.tt] = 0, q2[++q2.tt] = 0;
g[0] = INF;
for (int i = 1; i <= n; i++) {
vector<int> v;
i64 k = 2 * s;
g = INF;
while (q0.hh < q0.tt && y(q0[q0.hh + 1]) - y(q0[q0.hh]) <= k * (x(q0[q0.hh + 1]) - x(q0[q0.hh]))) q0.hh++;
while (q1.hh < q1.tt && y(q1[q1.hh + 1]) - y(q1[q1.hh]) <= k * (x(q1[q1.hh + 1]) - x(q1[q1.hh]))) q1.hh++;
while (q2.hh < q2.tt && y2(q2[q2.hh + 1]) - y2(q2[q2.hh]) <= k * (x(q2[q2.hh + 1]) - x(q2[q2.hh]))) q2.hh++;
int j = q0[q0.hh];
f = f[j] + sq(s - s[j] - L);
if (q0.hh < q0.tt) j = q0[q0.hh + 1], g = min(g, f[j] + sq(s - s[j] - L));
if (q0.hh) j = q0[q0.hh - 1], g = min(g, f[j] + sq(s - s[j] - L));
while (q0.hh < q0.tt && (y(q0[q0.tt]) - y(q0[q0.tt - 1])) * (x(i) - x(q0[q0.tt])) >= (y(i) - y(q0[q0.tt])) * (x(q0[q0.tt]) - x(q0[q0.tt - 1]))) v.emplace_back(q0[q0.tt--]);
reverse(v.begin(), v.end());
if (q1.hh <= q1.tt) j = q1[q1.hh], g = min(g, f[j] + sq(s - s[j] - L));
if (v.size()) while (q1.hh <= q1.tt && x(q1[q1.tt]) >= x(v[0])) q1.tt--;
for (auto o : v) {
while (q1.hh < q1.tt && (y(q1[q1.tt]) - y(q1[q1.tt - 1])) * (x(o) - x(q1[q1.tt])) >= (y(o) - y(q1[q1.tt])) * (x(q1[q1.tt]) - x(q1[q1.tt - 1]))) q1.tt--;
q1[++q1.tt] = o;
}
j = q2[q2.hh], g = min(g, g[j] + sq(s - s[j] - L));
while (q2.hh < q2.tt && (y2(q2[q2.tt]) - y2(q2[q2.tt - 1])) * (x(i) - x(q2[q2.tt])) >= (y2(i) - y2(q2[q2.tt])) * (x(q2[q2.tt]) - x(q2[q2.tt - 1]))) q2.tt--;
q0[++q0.tt] = q2[++q2.tt] = i;
}
cout << f[1] << &#39;\n&#39;;
for (int i = 2; i <= n; i++) cout << f << &#39; &#39; << g << &#39;\n&#39;;
return 0;
} |
|