|
|
本文出自我在学校的研究生讲座(graduate colloquium)的报告. 这个报告的目的是介绍一个组合对象:超平面排列。简单来说,设 K 是一个域,那么一个超平面排列就是一个偶对 \mathcal{V}:=(V,\eta) ,其中 V\subset K^n 是一个 d 维K -线性子空间,并且跟所有坐标超平面 H_i 都横截相交,而 \eta\in K^n/V 是一个向量. 我们称 d 为超平面排列的维数,记作 \dim\mathcal{V} .
注 一个更直接的定义是, \mathcal{V} =\{H_1 ,H_2,\dotsb ,H_n\} ,其中 H_i\subset K^d 是仿射超平面,即它是由余维数1的线性子空间平移得到的. 我们可以看到这两个定义是等价的(如果 \mathcal{V} 是本质的),而我们选取看起来比较不直观的前者作为定义的原因是在定义拟阵(matroid)或者可逆拟阵的时候,前者更加方便.
当我们选取 K=\mathbb{R} 的时候, \mathbb{R}^d 上的这些超平面将整个空间切分成不连通的部分,比如在二维的时候,我们有
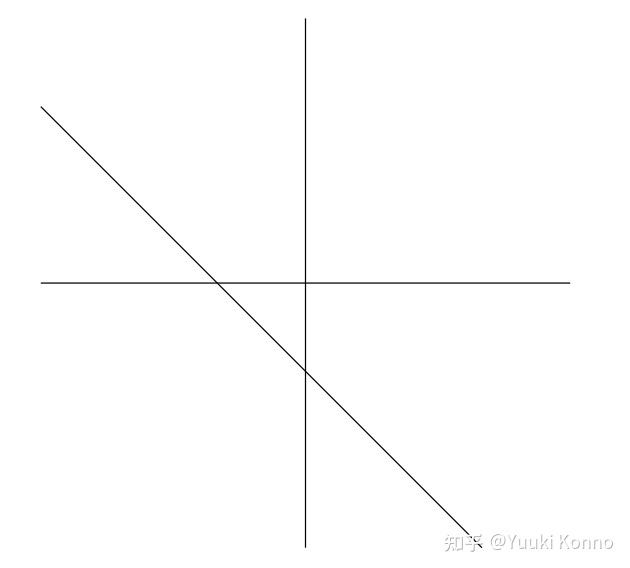
从上图我们可以看到在这种情况下, \mathbb{R}^2 被这三条直线切分成7个不同的区域,其中一个是紧的,即它的闭包在 \mathbb{R}^2 里面是紧的. 我们称这些区域为室(chamber). 一个趣味组合问题是:对给定的 \mathbb{R}^d 上的n个超平面,我们能否知道它有多少个室?有多少个紧的室?
定义 我们称一个超平面排列 \mathcal{V} 是本质的,如果它的所有超平面 H_i 在 V 中的法向量生成整个 V ;否则,我们说 \mathcal{V} 是不本质的. 空间 V\setminus\bigcup_{i=1}^n H_i 的连通分支称为一个室,其中 H_i =\{x\in\mathbb{R}^n\vert x_i=0\} 是坐标超平面.
如果 \mathcal{V} 是不本质的,那么我们可以找到一个投影 V\to V^e ,将每个超平面都同构地映到 V^e 上的一个超平面,使得投影后的超平面排列 \mathcal{V}^e 是本质的.
定义 我们称一个室是紧的,如果它在对应的本质化 \mathcal{V}^e 里面的像的闭包是紧的. 我们称本质化 \mathcal{V}^e 的维数为 \mathcal{V} 的秩,记作 \mathrm{rank}\ \mathcal{V} .
令 r(\mathcal{V}) 为 \mathcal{V} 里面的室的数量,而 b(\mathcal{V}) 为对应的紧室的数量. 为了计算这些数,我们尝试应用归纳法:如果我们看一维的超平面排列,它就是一条直线去掉数个不同的点:

(这里的圆圈代表去掉的点),从这张图我们就可以看出来下述结果:
命题 如果 \dim\mathcal{V}=1 ,那么 r(\mathcal{V})=n+1 并且 b(\mathcal{V})=n-1 .
在高维的时候,我们没有这种清楚的图像来帮助我们数室的个数,但是至少我们知道当 n=1 的情形:此时 \mathcal{V} 只有两个室,并且其本质化是一个一维直线上的一个点,从而我们知道它也没有任何紧的室,即在这种情况下我们有 r(\mathcal{V})=2 并且 b(\mathcal{V})=0 .
一般情形可以通过下述删节-限制归纳来计算:注意到对每个超平面排列 \mathcal{V} 和其中一个超平面 H ,我们可以考虑它的删节超平面排列 \mathcal{V}_H ,即将 H 从这些超平面里面去掉;以及它到 H 的限制 \mathcal{V}^H ,即考虑 H 作为底空间的一个超平面排列,其中每个超平面都是 H 与其它超平面的交. 假设我们已经知道了 r(\mathcal{V}_H) 和 r(\mathcal{V}^H) ,现在我们希望计算 r(\mathcal{V}) . 注意到超平面 H 将它经过的每一个室分割为了两部分,而其它室在把 H 加进去前后没有变化,因而差 r(\mathcal{V})-r(\mathcal{V}_H) 等于与 H 相交的所有室的个数,但这等于 H 里面的室的个数 r(\mathcal{V}^H) ,因此我们得到 r(\mathcal{V})=r(\mathcal{V}_H)+r(\mathcal{V}^H) . 对于紧室的情形,我们也可以做类似的递归,但注意到此时我们必须同时也去追踪它的秩,即加入超平面 H 是否改变 \mathcal{V}_H 的秩. 其结果为
命题 如果 \mathrm{rank}(\mathcal{V})=\mathrm{rank} (\mathcal{V}_H)+1 ,那么 b(\mathcal{V})=b(\mathcal{V}_H) ;否则,如果 \mathrm{rank} (\mathcal{V})=\mathrm{rank} (\mathcal{V}_H) ,那么 b(\mathcal{V})=b(\mathcal{V}_H)+b(\mathcal{V}^H) .
这个算法可以帮助我们,对于任何具体的情形计算出紧室和室的数量,但是一般地,我们希望在一些特殊情形下能得到一些漂亮的组合公式. 比如说
定义 我们称超平面排列 \mathcal{V} 处于一般位置,如果对任何 k 个超平面 H_{a_1} ,H_{a_2},\dotsb,H_{a_k} ,我们有 \mathrm{codim}\ H_{a_1}\cap H_{a_2}\cap\dotsb\cap H_{a_k} =k . 我们称 \mathcal{V} 是中心的,如果所有的超平面都经过一个给定的点. 换句话说,如果我们将这个点放到原点,那么 \mathcal{V} 是中心的等价于所有的超平面都是线性超平面.
前一种情形是一般情形:对任何超平面排列, 经过恰当的扰动我们总会得到一个处于一般位置的超平面排列;后者是最退化的情形。我们希望在这两种情形下能得到关于这两个数字的比较漂亮的组合公式. 为此,我们需要发掘超平面排列的更多组合信息.
定义 令 \mathcal{V} 是一个超平面排列,则我们定义它的相交偏序集(intersection poset) L(\mathcal{V}) 为一个偏序集,其中每个元素都是 \{0,1,\dotsb ,n\} 的子集 S ,对应于非空的相交超平面 H_S :=\bigcap_{i\in S} H_i . 记 H_{\emptyset} =V . L(\mathcal{V}) 上的偏序定义为集合之间的包含关系: S\leq T 当且仅当 S\subseteq T .
L(\mathcal{V}) 实际上是一个几何格:它上面有最大值 S\vee T 和最小值 S\wedge T 两种操作,它有一个极小元 \emptyset :=\bm{0} ,并且对任何元素 S\in L(\mathcal{V}) ,最长的链 S_0=\bm{0} <S_1<\dotsb <S_n=S 的长度是相同的. 对这样的几何格 L ,我们可以定义一个Möbius函数 \mu\colon L\times L\to\mathbb{Z} 为满足
- \mu (x,x)=1 对任何 x\in L ;
- \mu (x,y)=0 如果 x>y ;
- \sum_{x\leq z\leq y}\mu (x,z)=0 对任何 x,y,z\in L 成立;
的二元函数. 因为 L 有一个极小元,我们记 \mu (x)=\mu (\bm{0},x) 为对应的Möbius函数. 对给定的两个函数 f,g\colon L\times L\to\mathbb{Z} 满足 f(x,y)=g(x,y)=0 如果 x>y ,我们可以定义它们的卷积为 f\ast g(x,y):=\sum_{x\leq z\leq y} f(x,z)g(z,y) . Möbius函数具有下述性质:
定理 对任何两个函数 f,g\colon L\to\mathbb{Z} ,下列两个命题等价:
- f(x)=\sum_{y\geq x} g(y) 对任何 x\in L 成立;
- g(x)=\sum_{y\geq x}\mu(x,y) f(y)
上述定理也称为Möbius反演公式. 现在,对任何一个给定的超平面排列 \mathcal{V} 相交偏序集 L(\mathcal{V}) 里面的每个元素 x 在 V 里面对应的子空间的维数记作 \dim x ,我们定义它的特征多项式为 \chi_{\mathcal{V}} (t)=\sum_{x\in L(\mathcal{V})}\mu (x)t^{\dim x} . 这个特征多项式同样满足删节-限制归纳:
定理 如果 H\in\mathcal{V} 是超平面排列 \mathcal{V} 里面的一个超平面,则我们有 \chi_{\mathcal{V}} (t)=\chi_{\mathcal{V}_H} (t)-\chi_{\mathcal{V}^H} (t) .
室的数量 r(\mathcal{V}) 以及紧室的数量 b(\mathcal{V}) 实际上都是特征多项式在不同取值下的数字:
命题 r(\mathcal{V})=(-1)^d\chi_{\mathcal{V}} (-1) 并且 b(\mathcal{V})=(-1)^{\mathrm{rank}\mathcal{V}} \chi_{\mathcal{V}} (1) .
证明 一个最简单的证明是说明当 \dim\mathcal{V}=1 的时候这两个公式成立,然后其余情况可以由删节-限制递归直接得到. 一个更几何的证明如下:前面我们已经提到,一个超平面排列 \mathcal{V} 给出了 \mathbb{R}^d 的一个胞腔分解,并且对每个元素 x\in L(\mathcal{V})=L , \mathcal{V} 限制到 x 上给出 x 的一个超平面排列,而每个室对应到一个 \dim x 维的胞腔. 注意到 \chi (\mathbb{R}^d) =(-1)^d ,因此我们有 (-1)^d =\sum_{x\in L(\mathcal{V})} (-1)^{\dim x} r(\mathcal{V}\vert_x) . 注意到 \mathcal{V}\vert_x 也是一个超平面排列,因而我们有 (-1)^{\dim x} =\sum_{y\geq x}(-1)^{\dim y}r(\mathcal{V}\vert_y) . 根据上述Möbius反演公式,我们立刻得到 (-1)^dr(\mathcal{V})=\sum_x (-1)^{\dim x}\mu(x)=\chi_{\mathcal{V}} (-1) ,因此 r(\mathcal{V})=(-1)^d \chi_{\mathcal{V}} (-1) .
类似地,我们可以对 b(\mathcal{V}) 得到对应的公式. 但是这里我们需要证明 \mathcal{V}^e 上所有紧室的并 \Gamma 是可缩的,这并不显然,但是由可缩和紧性我们立刻得到 \chi (\Gamma)=1 . \square
现在我们来计算中心和一般位置超平面排列的情形.
命题 如果 \mathcal{V} 是一个中心超平面排列,那么 r(\mathcal{V})=2n 且 b(\mathcal{V})=0 .
这是限制-删节归纳的直接推论,读者可以留作习题.
命题 如果 \mathcal{V} 是一个一般位置超平面排列,那么 r(\mathcal{V})=1+n+\binom{n}{2}+\dotsb +\binom{n}{d} 且 b(\mathcal{V})=\binom{n-1}{d} . 它的特征多项式为 \chi_{\mathcal{V}} (t)=t^d -nt^{d-1}+\binom{n}{2}t^{d-2}-\dotsb+(-1)^d\binom{n}{d} .
这是下述Whitney定理的直接推论:
定理(Whitney) 若 \mathcal{V} 是一个 d 维超平面排列,那么 \displaystyle\chi_{\mathcal{V}} (t)=\sum_{\begin{subarray}{c}\mathcal{A}\subseteq\mathcal{V}\\\mathcal{A}\text{是中心的}\end{subarray}}(-1)^{\#\mathcal{A}}t^{n-\mathrm{rank}\mathcal{A}} .
这样我们就完成了在特殊例子下的计算.
现在来考虑另外一个问题:考虑 \mathbb{C}^d 里面的 n 个复超平面 \{H_1 ,H_2,\dotsb, H_n\} ,我们希望计算补空间 \displaystyle\mathbb{C}^d\setminus\bigcup_{i=1}^n H_i 的上同调环 \displaystyle H^{\ast} \left(\mathbb{C}^d\setminus\bigcup_{i=1}^n H_i\right) . Arnold和Brieskorn早年的工作说明了一些例子下这个上同调环由微分1-形式 \displaystyle\frac{\mathrm{d}\alpha_H}{\alpha_H} 生成,其中 \alpha_H 是定义超平面 H 的复线性函数. 这个结果实际上对一般的超平面排列都对:基本想法也是在上同调群上尝试做删节-限制归纳。对某个 H\in\mathcal{V} ,记 M(\mathcal{V}) 为补集 \displaystyle\mathbb{C}^d\setminus\bigcup_{i=1}^n H_i ,则我们有嵌入 M(\mathcal{V})\hookrightarrow M(\mathcal{V}_H) 以及 M(\mathcal{V}^H)\times\mathbb{C}\hookrightarrow M(\mathcal{V}_H) ,并且它们满足 M(\mathcal{V}_H) =M(\mathcal{V})\cup M(\mathcal{V}^H)\times\mathbb{C} . 因此由Mayer-Vietoris定理,我们得到上同调群的长正合列
\xrightarrow{+1} H^k M(\mathcal{V}_H)\to H^k M(\mathcal{V})\oplus H^k (M(\mathcal{V}^H)\times\mathbb{C})\to H^k (M(\mathcal{V}^H)\times\mathbb{C}^{\ast})\xrightarrow{+1}\dotsb
由Künneth定理,我们有 H^k (M(\mathcal{V}^H)\times\mathbb{C}^{\ast})\cong H^{k-1}M(\mathcal{V}^H)\oplus H^k M(\mathcal{V}^H) ,并且注意到映射 H^k M(\mathcal{V})\oplus H^k (M(\mathcal{V}^H)\times\mathbb{C})\cong H^k M(\mathcal{V})\oplus H^k M(\mathcal{V}^H)\to H^{k-1} M(\mathcal{V}^H)\oplus H^kM(\mathcal{V}^H) 分裂并且在第二个分量上是同构(因为这是由嵌入诱导的,我们不难看到这一点),我们可以将长正合列简化为
\xrightarrow{+1}H^kM(\mathcal{V}_H)\to H^k M(\mathcal{V})\to H^{k-1} M(\mathcal{V}^H)\to H^{k+1} M(\mathcal{V}_H)\to\dotsb
经过一些更多的计算,我们得到
命题 我们有短正合列 0\to H^k M(\mathcal{V}_H)\to H^k M(\mathcal{V})\to H^{k-1}M(\mathcal{V}^H)\to 0 .
这个结果给出了在上同调上的限制-删节归纳. |
|