|
|
等距变换(isometry)是保持距离不变的变换,任意两点之间的距离和它们在等距变换下的像之间的距离相等。
平面上的等距变换以变换的复合为乘法构成一个乘法群:
- 恒等变换是等距变换;
- 如果 f 是等距变换,那么 f^{-1} 也是等距变换;
- 如果 f 和 g 是等距变换,那么 f\circ g 也是等距变换,且三个变换的复合满足结合律。
下面提到的等距变换都是平面内的等距变换。
一、等距变换把直线变成直线
在欧几里得公理化几何体系下直接用定义证明三点共线很难,但把直线看成到两点等距的点的轨迹,去证明等距变换把直线变成直线就容易了。
对任意直线 l ,我们可以选择任意不在直线上的一点 P 以及 P 关于直线 l 的反射 Q ,那么直线 l 就成了线段 PQ 的垂直平分线。
对任意等距变换 f ,考虑 l 在 f 下的像 l'=f(l) ,记 P 和 Q 在 f 下的像分别为 P' 和 Q' ,我们证明 l' 正好就是线段 P'Q' 的垂直平分线。
一方面,对 l' 上的任意一点 A' ,一定有 A' 在 f 下的原像 A 在直线 l 上, A 到 P 和 Q 的距离相等。由于 f 是保距变换, A' 到 P' 和 Q' 的距离相等,因此 A' 在线段 P'Q' 的垂直平分线上。
另一方面,对 P'Q' 的垂直平分线上任意一点 A' ,有 A' 到 P' 和 Q' 的距离相等。考虑 A' 在 f 下的原像 A ,由 f 保距一定有 A 到 P 和 Q 的距离相等,也就是 A 在线段 PQ 的垂直平分线 l 上,也就说明了 A' 在 l' 上。
综上可得, 直线 l 在变换 f 下的像 l' 就是线段 P'Q' 的垂直平分线。
由此可以得到推论:
等距变换把共线的点映为共线的点,把不共线的点映为不共线的点。
二、不共线的三点确定一个等距变换
任意给定平面上的不共线的三个点 A , B 和 C . 如果这三个点在等距变换 f 和 g 下的像都分别为 A' , B' 和 C' ,那么这两个变换相等 f=g .
由第一部分的推论可知 A' , B' 和 C' 不共线。
用反证法,假设存在一点 P 在变换 f 和 g 下的像不相等,即 f(P)\neq g(P) ,考虑连接 f(P) 和 g(P) 两点的线段的垂直平分线 l' . 由等距变换的定义可得, 到 A'=f(A) 到 f(P) 的距离和 A'=g(A) 到 g(P) 的距离都等于 AP ,因此 A' 在垂直平分线 l' 上。同理可得 B' 和 C' 也在 l 上, A' , B' 和 C' 都在直线 l' 上,与这三点不共线矛盾。
三、基本等距变换——反射的定义及其对合性
平面内的任何一个反射都由一条直线决定,给定任意一条直线 l ,可以定义关于直线 l 的反射 r_l 为满足以下两个条件的变换:
- 保持 l 不动:对直线 l 上的任意一点 A ,都有 r_l(A)=A ;
- 原像与像到直线 l 等距:对不在直线 l 上的任意一点 A ,其像 A'=r_l(A) 也不在直线 l 上,并且有直线 l 是线段 AA' 的垂直平分线,也就是直线 l 上的点到 A 和 A' 的距离相等。
从平面几何知识可知2中的 A' 是存在且唯一的:过 A 作 l 的垂线 m 与 l 相交于点 P ,在 m 上恰好有一个点 A' ,使得线段 AA' 以 P 为中点。
通过分类讨论容易证明反射一定是等距变换。
用平面几何知识可证明反射是等距变换
根据定义容易得到:关于同一条直线反射两次得到的变换 r_l\circ r_l 是恒等变换,也就是反射具有对合性,反射 r_l 的逆是其本身 r^{-1}_l=r_{l} .
下面我们说明所有反射构成等距变换群里的生成元。
四、等距变换至多由三个反射复合而成
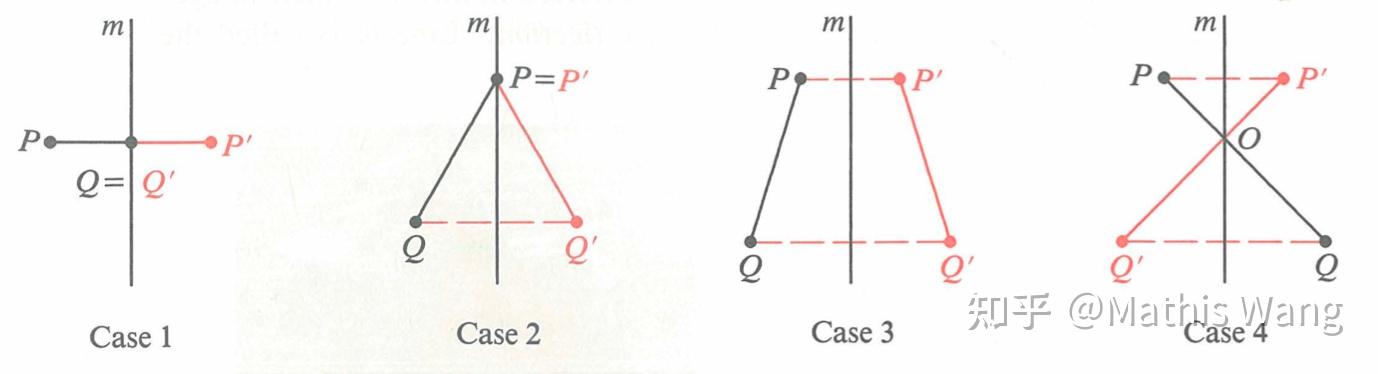
我们根据等距变换 f 的不动点个数来分类讨论:
情形1: f 有三个不共线的不动点,根据第二部分的结论知 f 就是恒等变换;
情形2: f 有两个不动点 A 和 B ,决定一条直线 l .
若 f 不是恒等变换,则存在点 P 使得 P'=f(P)\neq P . 由 A 和 B 是 f 的不动点且 f 等距,可知 AP=AP' , BP=BP' , 因此 A 和B 所在的直线 l 就是线段 PP' 的垂直平分线。
考虑由直线 l 决定的反射 r_l ,根据反射的定义一定有 r_l(P')=P .
注意到保距变换 r_l\circ f 有三个不共线的不动点:
r_l\circ f(P)=r_l(f(P))=r_l(P')=P
r_l\circ f(A)=r_l(f(A))=r_l(A)=A
r_l\circ f(B)=r_l(f(B))=r_l(B)=B
因此得到 r_l\circ f 是恒等变换,从而 f=r_l^{-1}=r_l 是关于两不动点所在直线的反射。
情形3: f 只有一个不动点 A .
若 f 不是恒等变换,则存在点 P 使得 P'=f(P)\neq P ,考虑线段 PP' 的垂直平分线 l .
因为 A 是 f 的不动点且 f 保距, AP=AP' ,因此 A 在垂直平分线 l 上。
保距变换 r_l\circ f 就有两个不动点:
r_l\circ f(P)=r_l(f(P))=r_l(P')=P
r_l\circ f(A)=r_l(f(A))=r_l(A)=A
这就回到了情形2,得到 r_l\circ f 要么是恒等变换,要么是反射 r_m . 结合 f 只有一个不动点推出 f 是两个反射的复合 r_l\circ r_m .
情形4: f 没有不动点.
任取一点 P ,其在 f 下的像 P'=f(P) ,同样考虑线段 PP' 的垂直平分线 l 和由此决定的反射 r_l .
保距变换 r_l\circ f(P)=r_l(f(P))=r_l(P')=P 有一个不动点,由情形3结论可知 r_l\circ f 要么是恒等变换,要么是反射 r_m ,要么是两个反射的复合 r_m\circ r_n . 结合 f 没有不动点可推出 f 要么是两个反射的复合 r_l\circ r_m ,要么是三个反射的复合 r_l\circ r_m\circ r_n .
综上所述,任何等距变换都至多由三个反射复合而成,总结如下:
- 等距变换如果有三个不共线的不动点,就一定是恒等变换;
2. 如果有两个不动点,且不是恒等变换,就一定是反射,且两个不动点决定的直线是反射线(不动直线);
3. 如果只有一个不动点,一定是两个反射的复合(这两个反射对应的直线相交,复合得到旋转);
4. 如果没有不动点,要么是两个反射的复合(这两个反射对应的直线平行,复合得到平移),要么是三个反射的复合(是平移反射)。
下一篇文章展开论述第3条和第4条的前半部分:给出平移和旋转的定义和相互之间的复合、刚体运动群及其坐标/向量表示。 |
|