|
|
上期回顾
说明
本文中的定理性质内容较多,后续会给出证明,当然笔者遇到有趣的性质也会随时补充
一、内心
1.定义[1]:
内心(Incenter),三角形三条内角角平分线的交点叫三角形的内心,即内切圆的圆心。
2.如何证明三角形的三条内角角平分线交于一点?
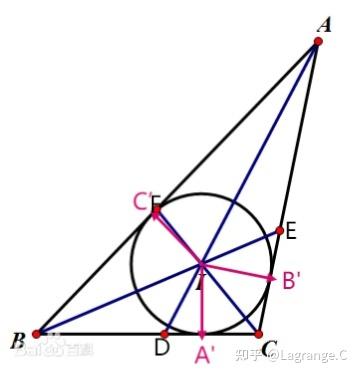
三角形的内心I
过I作三边的垂线分别交于A',B',C'.由角平分线性质可知:IA'=IB'=IC'(斯霍腾定理),易证 IC'\bot AB,IB'\bot AC,IA'\bot BC .综上所述易得I为内切圆的圆心
3.性质[2]
1、三角形的三个角平分线交于一点,该点即为三角形的内心。
2、三角形的内心与三角形位置关系:现有AI交BC于点D;BI交CA于点E;CI交AB于点F,三角形内接圆分别交BC,CA,AB于X,Y,Z。
(1) IX=IY=IZ
(2) \frac{BD}{CD}=\frac{b}{c} (角平分线定理)
(3) \frac{BX}{CX}=\frac{p-b}{p-c} ,其中 p=\frac {a+b+c}{2} 为半周长
(4) \color{Blue}{AI:BI:CI=\frac{1}{sin\frac{A}{2}}:\frac{1}{sin\frac{B}{2}}:\frac{1}{sin\frac{C}{2}}}
(5) \color{Blue}{S_\Delta IBC:S_\Delta ICA:S_\Delta IAB=a:b:c}
3、 r=\frac{p}{3}
4、若 C=90° ,则 r=\frac{a+b-c}2
5、对于4、有更普遍的结论 \color{Blue}{ r=\frac{tan\frac A2 (b+c-a)}2}
6、(O是平面ABC上任意一点) O是\Delta ABC的内心\Leftrightarrow \color{Blue}{\overrightarrow{OA} +\overrightarrow{OB} +\overrightarrow{OC} =\overrightarrow{0} }
7. (点O是平面ABC上任意一点)点O是△ABC内心\Leftrightarrow \overrightarrow{OI}= \frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{a+b+c}
8、 I_x=\frac{A_x+B_x+C_x}{3},I_y=\frac{A_y+B_y+C_y}{3}
9、(欧拉定理) \bigtriangleup ABC中,R,r分别为外接圆\odot O半径和内接圆\odot I半径 ,则\color{Blue}{OI^2=R^2-2Rr}
<hr/>二、外心
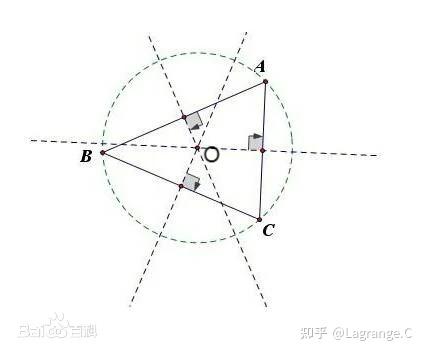
外心
定义:指三角形三条边的垂直平分线(中垂线)的相交点。用这个点做圆心可以画三角形的外接圆。指三角形外接圆的圆心,一般叫三角形的外心。三角形的外心是三边中垂线的交点,且这点到三角形三顶点的距离相等。外心是三角形三条边的垂直平分线的交点,即外接圆的圆心。[3] 1.关于“三角形的三边的垂直平分线交于一点”的证明:
注意到外心到三角形的三个顶点距离相等,结合垂直平分线性质,外心定理其实极好证。
计算外心的坐标是一件麻烦的事。先计算下列临时变量:
d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
(例如: d_1=\overrightarrow{AB} ·\overrightarrow{AC} )
记 c1=d2×d3,c2=d1×d3,c3=d1×d2,c=c1+c2+c3 。
外心坐标: ( \frac{c_2+c_3}{2c},\frac{c_3+c_1}{2c},\frac{c_1+c_2}{2c} ) 。
2.性质
1、锐角三角形的外心在三角形内; 直角三角形的外心在斜边上,与斜边中点重合; 钝角三角形的外心在三角形外。
2、三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心,外心到三顶点的距离相等。
3、点G是平面ABC上一点,那么点G是⊿ABC外心的充要条件: {\color{Blue} {(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{AB}=(\overrightarrow{OB}+\overrightarrow{OC})·\overrightarrow{BC}=(\overrightarrow{OC}+\overrightarrow{OA})·\overrightarrow{CA}=\overrightarrow{0}} }
<hr/>三、重心
1.定义:三角形重心是三角形三条中线的交点。当几何体为匀质物体时,重心与[4]重合。
2.性质:
1、重心到顶点的距离与重心到对边中点的距离之比为2:1
2、重心和三角形3个顶点组成的3个三角形面积相等
3 {\color{Blue}{重心到三角形3个顶点距离平方的和最小}}
4、三角形内到三边距离之积最大的点
5、卡诺重心定理:若G为三角形ABC的重心,P为三角形ABC所在平面上任意一点,则 \color{blue}{PA^2+PB^2+PC^2=GA^2+GB^2+GC^2+3PG^2=\frac{1}{3} (a^2+b^2+c^2)+3PG^2}
6. \color{blue}{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}}
对于3的证明(参考自李永乐的解析几何):
设 P(x,y) 是平面ABC内一点,易知 PA=\sqrt[]{(x-x_A)^2+(y-y_A)^2} ,则 PA^2={(x-x_A)^2+(y-y_A)^2} ,同理 PB^2={(x-x_B)^2+(y-y_B)^2} , PC^2={(x-x_C)^2+(y-y_C)^2} .所以综上三式,重心到三角形3个顶点距离平方的和可以表示为:S=\color{Blue}{{(x-x_A)^2+(y-y_A)^2}} + {\color{Green} {(x-x_B)^2+(y-y_B)^2}} +{\color{Red} {(x-x_C)^2+(y-y_C)^2}}
展开整理可得 S=\color{Blue} {3x^2-2(x_A+x_B+x_C)x+(x_A^2+x_B^2+x_C^2)}+\color{Red} {3y^2-2(y_A+y_B+y_C)x+(y_A^2+y_B^2+y_C^2)}
当S最小时,蓝色和红色部分分别最小,即在这两条抛物线的对称轴上取到最小值,即
x=\frac{x_A+x_B+x_C}{3} ,y=\frac{y_A+y_B+y_C}{3} .命题获证!(性质4的证明类似)
<hr/>四、垂心
1.定义:垂心是从三角形的各个顶点向其对边所作的三条垂线的交点。
2.性质:
(1)锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部。
(2)三角形三个顶点,三个垂足,垂心这7个点可以得到6组四点共圆。
下面的性质是最为锐利重要的:
(3)三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
(4)垂心H关于三边的对称点,均在△ABC的外接圆上。
(5)H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为垂心组)
(6) △ABC,△ABH,△BCH,△ACH 的外接圆是等圆
(7)在非直角三角形中,过H的直线交AB、AC所在直线分别于P、Q,则 \frac{AB}{AP}·tanB+\frac{AC}{AQ} ·tanC=tanA+tanB+tanC
(8)设O,H分别为 △ABC 的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA
(9)锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍
(10)锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短(施瓦尔兹三角形,最早在古希腊时期由海伦(想不到吧)发现)。
(11)西姆松定理(西姆松线):从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上
(12)设锐角△ABC内有一点P,那么P是垂心的充分必要条件是 PB·PC·BC+PB·PA·AB+PA·PC·AC=AB·BC·CA
(13)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。(“垂心伴随外接圆,必有平行四边形”)
推论(垂心余弦定理):锐角三角形ABC的垂心为H,则 \frac{AH}{cosA} =\frac{BH}{cosB}=\frac{CH}{cosC}=2R (可引入有向距,推广到任意三角形)
(14) \overrightarrow{OA}·\overrightarrow{OB}=\overrightarrow{OB}·\overrightarrow{OC}=\overrightarrow{OC}·\overrightarrow{OA}
3.垂心坐标公式: \frac {y_2-y_1}{x_2-x_1}=-(x_3-x_G)
<hr/>更新(2022.9.1):
如图, \triangle ABC 的外心为 O ,重心为 G ,垂心为 H
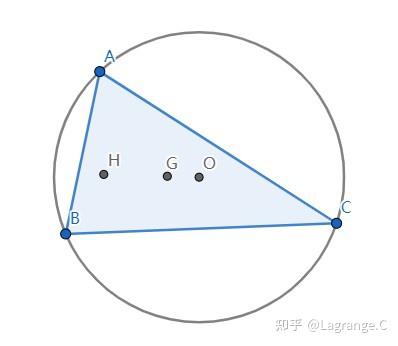
灵感来源:《奥数教程》
定理1: \overrightarrow{OH}= \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}
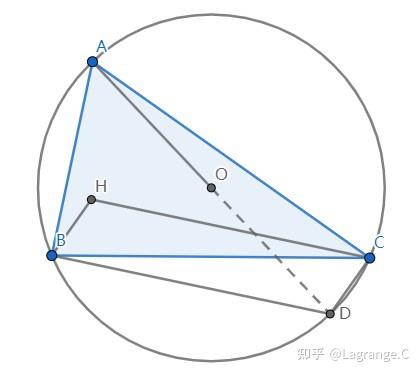
方法有一定的技巧
证明:过点 A 作圆的直径 AD ,由“直径所对的圆周角是直角”可得:
AB\bot BD,AC\bot CD
再由垂心本身的性质可得:
AB\bot CH,AC\bot BH
由“垂直于同一直线的两条直线互相平行”可得:
BD||CH,CD||BH
明显上述四条线段构成了平行四边形,所以:
BD=CH,CD=BH
引入向量可得:
\overrightarrow{BH}= \overrightarrow{DC}=\overrightarrow{OC}-\overrightarrow{OD}
注意到 \overrightarrow{OA},\overrightarrow{OD} 模长相等且方向相反,所以:
\overrightarrow{OA}=-\overrightarrow{OD}
所以: \overrightarrow{BH}=\overrightarrow{OC}-\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{OA}
因为 \overrightarrow{OB}+\overrightarrow{BH}=\overrightarrow{OH}
所以 \overrightarrow{OH}= \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} . Q.E.D.
定理2: \overrightarrow{OH}= \frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})
证明:

一行证明: \overrightarrow{OG}=\overrightarrow{OA}-\overrightarrow{GA}=\overrightarrow{OA}+\frac{2}{3}\overrightarrow{AD}=\overrightarrow{OA}+\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})=\overrightarrow{OA}+\frac{1}{3}(\overrightarrow{OB}-\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OA})=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})
定理3: O,G,H 三点共线,且 G 是 OH 邻 O 的三等分点
证明:结合定理1与定理2即证。
参考
- ^参考自wiki百科
- ^参考自百度百科
- ^张敬坤. 三角形外心的两个性质[J]. 数学通讯, 2010(4):45-46.
- ^面的形心就是截面图形的几何中心,质心是针对实物体而言的,而形心是针对抽象几何体而言的,对于密度均匀的实物体,质心和形心重合。 n 维空间中一个对象X的几何中心或形心是将X分成矩相等的两部分的所有超平面的交点。非正式地说,它是X中所有点的平均。如果一个物件质量分布平均,形心便是重心。
|
|