数学分析—16.1 平面点集与多元函数

废柴键盘

多元函数是一元函数的推广，因此它保留着一元函数的许多性质，但也由于自变量由一个增加到了多个，产生了一些新的性质。下面我们着重讨论二元函数，因为在掌握了二元函数的有关理论和研究方法之后，我们可以将它们推广到一般的多元函数中去。
一元函数的定义域是实数轴上的点集，二元函数的定义域将是坐标平面上的点集。因此，在讨论二元函数之前，有必要先了解有关平面点集的一些基本概念。
16.1.1  平面点集

由平面解析几何知道，当平面上确定了一个坐标系之后，所有有序实数对 (x,y) 与平面上的所有点之间建立了一一对应的关系。将这种确定了坐标系的平面，称为坐标平面。
坐标平面上满足某种条件 P 的点的集合称为平面点集，并记作
E=\{(x,y)\ |\ (x,y)\ 满足条件\ P\}\\平面点集\{(x,y)\ |\ (x-x_0)^2+(y-y_0)^2<\delta^2\}\\与
\{(x,y)\ |\ |x-x_0|<\delta,\ |y-y_0|<\delta\}\\分别称为以点 A(x_0,y_0) 为中心的 \delta 圆邻域和 \delta 方邻域（如图 1所示）。



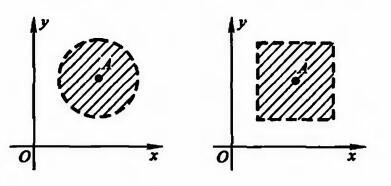
图  1

由于点 A 的任一圆邻域可以包含在点 A 的某一方邻域内，反之亦然，因此通常用“点 A 的 \delta 邻域”或“点 A 的邻域”来泛指这两种形状的邻域，并用记号 U(A;\delta) 或 U(A) 来表示。
点 A 的空心邻域是指
\{(x,y)\ |\ 0<(x-x_0)^2+(y-y_0)^2<\delta^2\}\\或
\{(x,y)\ |\ |x-x_0|<\delta,\ |y-y_0|<\delta,\ (x,y)\neq(x_0,y_0)\}\\并用记号 U^{\circ}(A;\delta) 或 U^{\circ}(A) 来表示。
下面我们可以从两个角度来描述点与点集之间的关系，第一个角度是按照“点 A 在 E 内或在 E 外”来进行定义。
任意一点 A\in\mathbb{R}^2 与任意一个点集 E\subset\mathbb{R}^2 之间必有以下三种关系之一：
（i）内点——若存在点 A 的某邻域 U(A) ，使得 \color{blue}{U(A)\subset E} ，则称点 A 是点集 E 的内点。 E 的全体内点构成的集合称为 E 的内部，记作 \text{int}\ E 。
（ii）外点——若存在点 A 的某邻域 U(A) ，使得 \color{blue}{U(A)\cap E=\varnothing}，则称 A 是 E 的外点。
（iii）边界点——若存在点 A 的任何邻域内既包含有属于 E 的点，又含有不属于 E 的点，则称 A 是 E 的边界点。即对任何正数 \delta ，恒有
\color{blue}{U(A;\delta)\cap E\neq \varnothing\  \wedge\  U(A;\delta)\cap E^c\neq \varnothing,}\\其中 E^c=\mathbb{R}^2\backslash E 是 E 关于全平面的补集。E 的全体边界点构成 E 的边界，记作 \partial E 。
注：E 的内点必定属于 E ， E 的外点必定不属于 E ， E 的边界点可能属于 E ，也可能不属于 E 。
下面我们从第二个角度来定义点与点集之间的关系，即按在点 A 的近旁是否密集着 E 中无穷多个点来进行区分：
（i）聚点——若在点 A 的任何空心邻域 U^{\circ}(A) 内都含有 E 中的点，则称 A 是 E 的聚点，即对于任意的正数 \delta ， \color{red}{U^{\circ}(A;\delta)\cap E\neq \varnothing} 。聚点本身可能属于 E ，也可能不属于 E 。
（ii）孤立点——若点 A\in E ，但不是 E 的聚点，即存在某一正数 \delta ，使得
\color{red}{U^{\circ}(A;\delta)\cap E= \varnothing,}\\
则称点 A 是 E 的孤立点。
注：孤立点一定是边界点，内点和非孤立的边界点一定是聚点，既不是聚点，也不是孤立点，则必为外点。
[例  1]  设平面点集
D=\{(x,y)\ |\ 1\leq x^2+y^2<4\}.\\满足 1< x^2+y^2<4 的一切点都是 D 的内点，满足 x^2+y^2=1 的一切点是 D 的边界点，它们都属于 D ，满足 x^2+y^2=4 一切点也是 D 的边界点，但它们都不属于 D，点集 D 连同它外圆边界上的所有点都是 D 的聚点。

根据点集中点的特征，我们再来定义一些重要的平面点集。
开集——若平面点集所属的每一点都是 E 的内点（即 \color{green}{\text{int}\ E=E} ），则称 E 为开集。
闭集——若平面点集 E 的所有聚点都属于 E ，则称 E 为闭集。
开域——若非空开集 E 具有连通性，即 E 中任意两点之间都可以用一条完全包含于 E 的有限折线（由有限条直线段连接而成的折线）相连接，则称 E 为开域（即开域就是非空连通开集）。
闭域——开域连同其边界构成的点集称为闭域。

华东师范大学数学系. 数学分析—下册[M]. 北京：高等教育出版社，2010.

冷面书生

锄禾日当午，发帖真辛苦。谁知坛中餐，帖帖皆辛苦！